Positive tests, admissions and deaths graphs from Christopher Bowyer (6 October)

By Hector DrummondCovid-19, Government, Health, Health fascism

Hector Drummond Magazine reader and contributor Christopher Bowyer has done some more Covid-19 test result graphs based on the data at https://coronavirus.data.gov.uk/. The data was downloaded yesterday, 6 October, so it’s very up-to-date. (All graphs can be clicked to enlarge.)

First, a health warning. The positive test data comes from PHE/NHS Track and Trace, and you’ll have seen very recently that their competence is questionable (to put it diplomatically). So take it with a grain of salt.

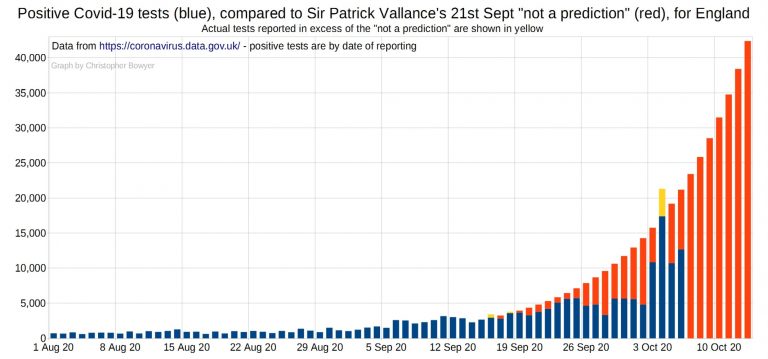
First up, a comparison of the current positive test situation with that ‘predicted’  by Vallance and Whitty on September 21 – this version is adjusted to apply to England only to match the charts below (which are England only).

 

 

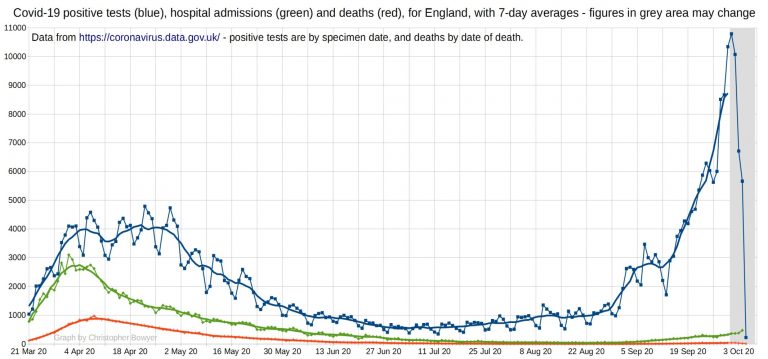
The following graph looks at SARS-CoV-2 positive tests (blue), Covid hospital admissions (green), and Covid deaths (red) for England. You can see that there’s been a slight increase in hospital admissions over September, as expected given the time of year, but it’s hardly a public health disaster in the making. They’re also not rising exponentially, but are fairly flat. The number of deaths is still very small, and and has also been pretty flat recently.

 

 

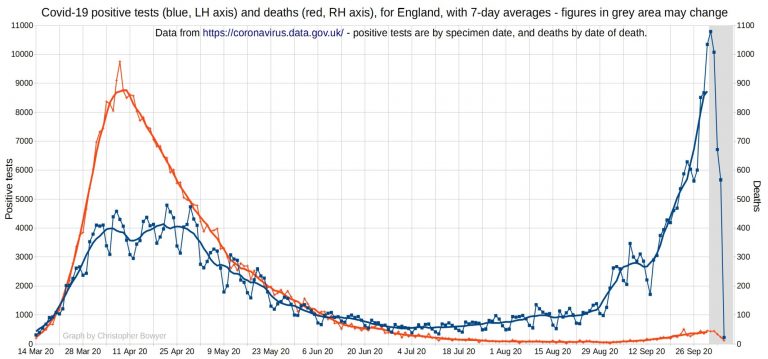
English SARS-CoV-2 positive tests (blue) and Covid-19 deaths (red). This graph uses a different scale than the last graph for deaths so you get a closer look at them. You can see that there has been an increase in deaths recently, but only very a slight one, so clearly the large increase in positive tests over August and September has not been matched by anything like that with deaths.

 

 

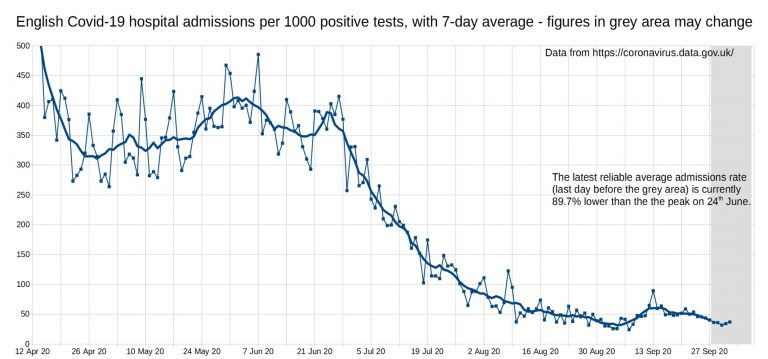
Hospital admissions per 1000 positive tests, England. Still nothing to worry about there. Why didn’t Witless and Unballanced present this sort of data?

 

 

A couple of new graphs now – Christopher says “to look at things other than positive tests – after the spreadsheet fiasco, the positive test data is at best questionable”.

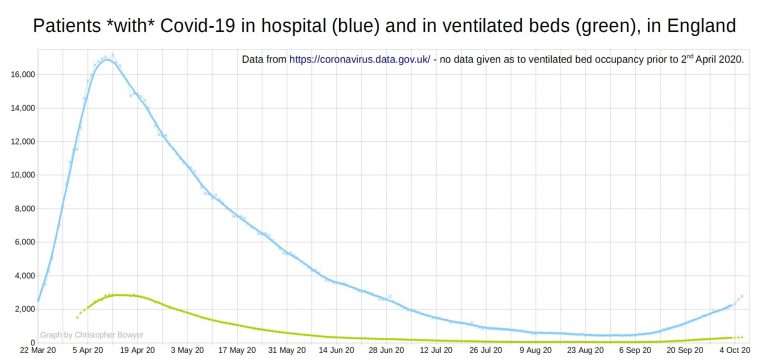
The first new graph

shows the patients with covid in hospital and in ventilated beds – I don’t know if this means they’re on a ventilator, or in ICU – it’s just what the data is called on https://coronavirus.data.gov.uk/healthcare?areaType=nation&areaName=England

 

 

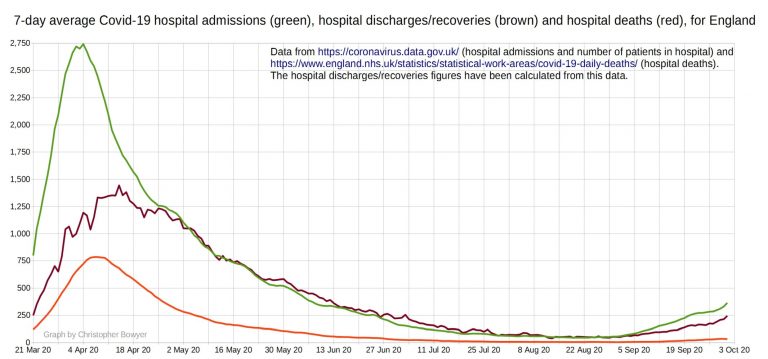
The second new graph is of Covid hospital admissions, Covid hospital discharges (recoveries) and Covid hospital deaths. Christopher says:

I was able to calculate the hospital discharges myself from the patients in hospital data and admissions data on the coronavirus.data.gov.uk website, and the NHS England hospital deaths data.

It’s not perfect, the discharges figure jumps around a fair bit from day to day – hence I’ve only plotted the 7-day averages on the graph, to smooth this out a bit.

But as I often see people saying why doesn’t the government publish the recoveries figures, this might be the next best thing. Especially as on every single day I have data for, the average discharges figure has always been above the average deaths figure – if you go into hospital with Covid you’re much more likely to recover than die!

 

Share this article on social media:
fb-share-icon
Tweet
fb-share-icon

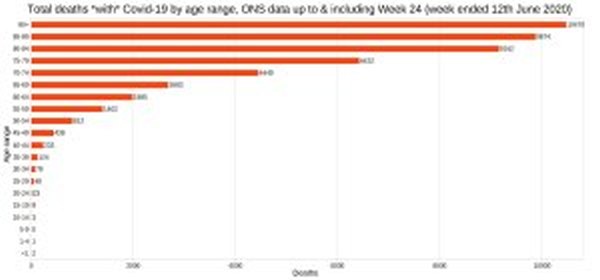
4 thoughts on “Positive tests, admissions and deaths graphs from Christopher Bowyer (6 October)”

  1. Underlying any analysis is the long-standing uncertainty about what a ‘Covid’ admission/hospitalisation/death actually means.

    It’s the old one about the difference between deaths ‘with’ and ‘of’ Covid – but, because of the ramifications of what we now know about the flaws inherent in PCR testing, the whole area of definition of a ‘Covid’ patient becomes highly questionable.

    In simple terms – we simply don’t know what the numbers show, in any context.

    It’s an unholy mess.

  2. Thanks for this analysis. I agree with Rick Hayward, the data is a mess and I would add that it appears to be constructed to generate and support head lines rather than allow informed decision making and risk management.

  3. Pingback: ‘Licence To Kill British Activists’ UK Secret Services Get Get Out Of Jail For Murder Card – Extraordinary Extradition: Britons Will Become Slaves The Day Julian Assange Dies Or Is ExtraditedNOT The BCfm Politics Show presented by Tony G

  4. New Good Article on Positive PCR Tests

    Might Most Positive Test be Wrong?
    …A lot of people are bad with numbers, and especially so in the area of probability…
    … For example, if the incidence of a disease in the population is 0.1% and the test has a false positive rate of 5%, the probability that a randomly-selected individual testing positive actually has the disease is approximately one in fifty: about 2%, or a probability of 0.02.

    Though this is easy to demonstrate, it is remarkable how resistant many perfectly intelligent people are to the conclusion, even when shown the proof. “But the test is 95% reliable”, they protest. “How can it be that a person with a positive test has anything less than a 95% chance of having the disease?”

    That kind of response merits attention. It does so because it is an example of an important failure to understand relevant data (and/or the terminology used to describe those data); and it is a failure that renders people blind (or, worse, resistant) to legitimate concerns about the significance of the published results of recent mass testing – concerns that are still not receiving the wider public attention that they deserve.

    This is a very clear explanation of the problem. Worth reading in full.”

    “…What is the false positive rate? Again, no one knows. The best estimate we have is from a meta-analysis by Andrew Cohen and Bruce Kessel of external quality assessments of RT-PCR assays of RNA viruses dating between 2004 and 2019. This analysis revealed false positive rates of 0-16.7%, with an interquartile range of 0.8-4.0% and a median of 2.3%

    …Suppose, for the sake of illustration again, that we take the median figure of 2.3% for the FPR, and run the same experiment as before: we test 100,000 people randomly picked from our population.

    Since the incidence is 1089 (rounded up) per 100,000, we should expect 1089 people to be positive. 98,911 are negative.
    Since the false positive rate is 2.3%, 2,274 (rounded down) of those 98,911 uninfected individuals will test positive.
    The total positive tests will therefore (assuming no false negatives) be 1089 + 2,274 = 3,363.

    If you have a positive test, therefore, it represents no more than a 1,089 over 3,363 chance – or 32.4% – that you are actually infected..

    …Government figures blithely assume that all positive tests represent real infected people, and ignore the huge distortion that even small proportions of false positive tests can make to any realistic estimate of incidence of infection in a community. My aim is only to assist the wider public understanding of just how dramatically the reliability of a positive test can be undermined by low percentages of false positives…

    …What is clear is that the public at large is currently blind to the very real possibility that the reliability of a positive test is significantly less than 100%; and that (deplorably) neither Government nor the mainstream media are doing anything to inform the public about such matters, which have an enormous and obvious significance for the moral and practical legitimacy of public policy measures being adopted in response to the testing data”
    https://lockdownsceptics.org/might-most-positive-tests-be-wrong/

    In some ways he makes it more complicated by being more accurate. I will stick with X% of tests will be FPs and if total “cases” lower than X% of tested, vast majority are FPs imprisoned for 14 days when innocent – thoughts?

Comments are closed.